Convolutional Sparse Coding with Mask Decoupling (ADMM)#
This example demonstrates the solution of a convolutional sparse coding problem
where the \(\mathbf{h}\)_k is a set of filters comprising the dictionary, the \(\mathbf{x}\)_k is a corrresponding set of coefficient maps, \(\mathbf{y}\) is the signal to be represented, and \(B\) is a cropping operator that allows the boundary artifacts resulting from circular convolution to be avoided. Following the mask decoupling approach [3], the problem is posed in ADMM form as
.
The most computationally expensive step in the ADMM algorithm is solved using the frequency-domain approach proposed in [53].
[1]:
import numpy as np
import scico.numpy as snp
from scico import plot
from scico.examples import create_conv_sparse_phantom
from scico.functional import L1MinusL2Norm, ZeroFunctional
from scico.linop import CircularConvolve, Crop, Identity, Sum
from scico.loss import SquaredL2Loss
from scico.optimize.admm import ADMM, G0BlockCircularConvolveSolver
from scico.util import device_info
plot.config_notebook_plotting()
Set problem size and create random convolutional dictionary (a set of filters) and a corresponding sparse random set of coefficient maps.
[2]:
N = 121 # image size
Nnz = 128 # number of non-zeros in coefficient maps
h, x0 = create_conv_sparse_phantom(N, Nnz)
Normalize dictionary filters and scale coefficient maps accordingly.
[3]:
hnorm = np.sqrt(np.sum(h**2, axis=(1, 2), keepdims=True))
h /= hnorm
x0 *= hnorm
Convert numpy arrays to jax arrays.
[4]:
h = snp.array(h)
x0 = snp.array(x0)
Set up required padding and corresponding crop operator.
[5]:
h_center = (h.shape[1] // 2, h.shape[2] // 2)
pad_width = ((0, 0), (h_center[0], h_center[0]), (h_center[1], h_center[1]))
x0p = snp.pad(x0, pad_width=pad_width)
B = Crop(pad_width[1:], input_shape=x0p.shape[1:])
Set up sum-of-convolutions forward operator.
[6]:
C = CircularConvolve(h, input_shape=x0p.shape, ndims=2, h_center=h_center)
S = Sum(input_shape=C.output_shape, axis=0)
A = S @ C
Construct test image from dictionary \(\mathbf{h}\) and padded version of coefficient maps \(\mathbf{x}_0\).
[7]:
y = B(A(x0p))
Set functional and solver parameters.
[8]:
λ = 1e0 # l1-l2 norm regularization parameter
ρ0 = 1e0 # ADMM penalty parameters
ρ1 = 3e0
maxiter = 200 # number of ADMM iterations
Define loss function and regularization. Note the use of the \(\ell_1 - \ell_2\) norm, which has been found to provide slightly better performance than the \(\ell_1\) norm in this type of problem [54].
[9]:
f = ZeroFunctional()
g0 = SquaredL2Loss(y=y, A=B)
g1 = λ * L1MinusL2Norm()
C0 = A
C1 = Identity(input_shape=x0p.shape)
Initialize ADMM solver.
[10]:
solver = ADMM(
f=f,
g_list=[g0, g1],
C_list=[C0, C1],
rho_list=[ρ0, ρ1],
alpha=1.8,
maxiter=maxiter,
subproblem_solver=G0BlockCircularConvolveSolver(check_solve=True),
itstat_options={"display": True, "period": 10},
)
Run the solver.
[11]:
print(f"Solving on {device_info()}\n")
x1 = solver.solve()
hist = solver.itstat_object.history(transpose=True)
Solving on CPU
Iter Time Objective Prml Rsdl Dual Rsdl Slv Res
----------------------------------------------------------
0 5.02e-01 1.836e+04 1.916e+02 2.736e+03 0.000e+00
10 8.78e-01 3.178e+03 6.317e+00 3.708e+01 7.611e-06
20 1.02e+00 2.910e+03 2.659e+00 1.703e+01 8.458e-06
30 1.16e+00 2.813e+03 1.857e+00 1.499e+01 8.146e-06
40 1.30e+00 2.747e+03 1.477e+00 7.850e+00 5.407e-06
50 1.44e+00 2.707e+03 1.221e+00 8.313e+00 6.305e-06
60 1.57e+00 2.676e+03 1.069e+00 8.159e+00 3.528e-06
70 1.70e+00 2.649e+03 9.734e-01 5.135e+00 2.572e-06
80 1.83e+00 2.627e+03 9.067e-01 4.549e+00 4.667e-06
90 1.98e+00 2.608e+03 8.483e-01 5.053e+00 5.881e-06
100 2.11e+00 2.589e+03 8.028e-01 4.263e+00 2.813e-06
110 2.25e+00 2.574e+03 7.621e-01 3.256e+00 2.696e-06
120 2.39e+00 2.559e+03 7.252e-01 3.335e+00 2.969e-06
130 2.52e+00 2.546e+03 6.985e-01 3.336e+00 2.951e-06
140 2.66e+00 2.533e+03 6.743e-01 2.813e+00 4.731e-06
150 2.80e+00 2.521e+03 6.524e-01 2.625e+00 5.164e-06
160 2.94e+00 2.510e+03 6.312e-01 2.687e+00 4.955e-06
170 3.07e+00 2.500e+03 6.087e-01 2.499e+00 3.436e-06
180 3.21e+00 2.490e+03 5.845e-01 2.297e+00 6.164e-06
190 3.34e+00 2.481e+03 5.612e-01 2.236e+00 5.721e-06
199 3.47e+00 2.474e+03 5.380e-01 2.158e+00 6.410e-06
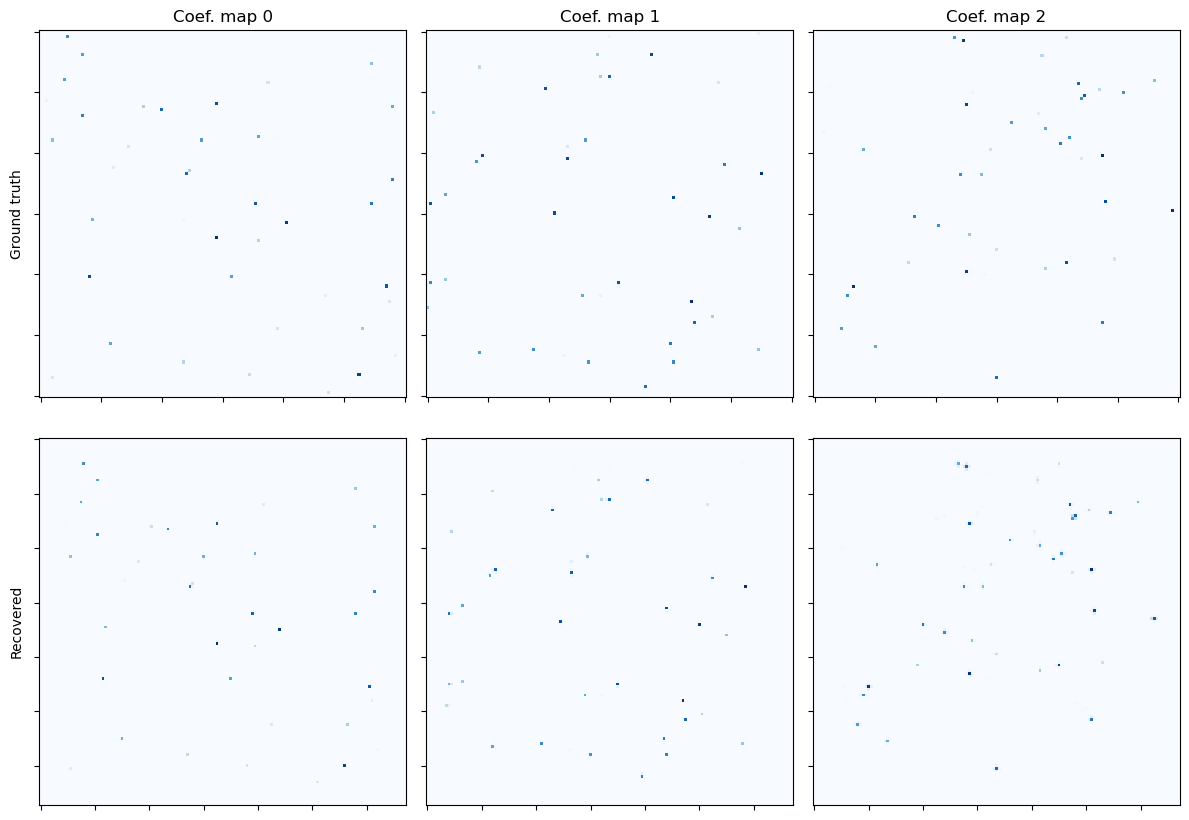
Show the recovered coefficient maps.
[12]:
fig, ax = plot.subplots(nrows=2, ncols=3, figsize=(12, 8.6))
plot.imview(x0[0], title="Coef. map 0", cmap=plot.cm.Blues, fig=fig, ax=ax[0, 0])
ax[0, 0].set_ylabel("Ground truth")
plot.imview(x0[1], title="Coef. map 1", cmap=plot.cm.Blues, fig=fig, ax=ax[0, 1])
plot.imview(x0[2], title="Coef. map 2", cmap=plot.cm.Blues, fig=fig, ax=ax[0, 2])
plot.imview(x1[0], cmap=plot.cm.Blues, fig=fig, ax=ax[1, 0])
ax[1, 0].set_ylabel("Recovered")
plot.imview(x1[1], cmap=plot.cm.Blues, fig=fig, ax=ax[1, 1])
plot.imview(x1[2], cmap=plot.cm.Blues, fig=fig, ax=ax[1, 2])
fig.tight_layout()
fig.show()
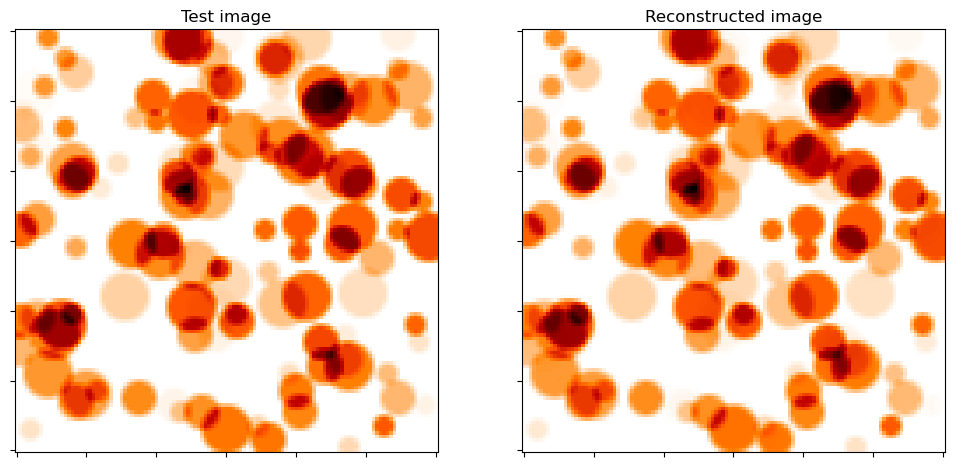
Show test image and reconstruction from recovered coefficient maps. Note the absence of the wrap-around effects at the boundary that can be seen in the corresponding images in the related example.
[13]:
fig, ax = plot.subplots(nrows=1, ncols=2, figsize=(12, 6))
plot.imview(y, title="Test image", cmap=plot.cm.gist_heat_r, fig=fig, ax=ax[0])
plot.imview(B(A(x1)), title="Reconstructed image", cmap=plot.cm.gist_heat_r, fig=fig, ax=ax[1])
fig.show()
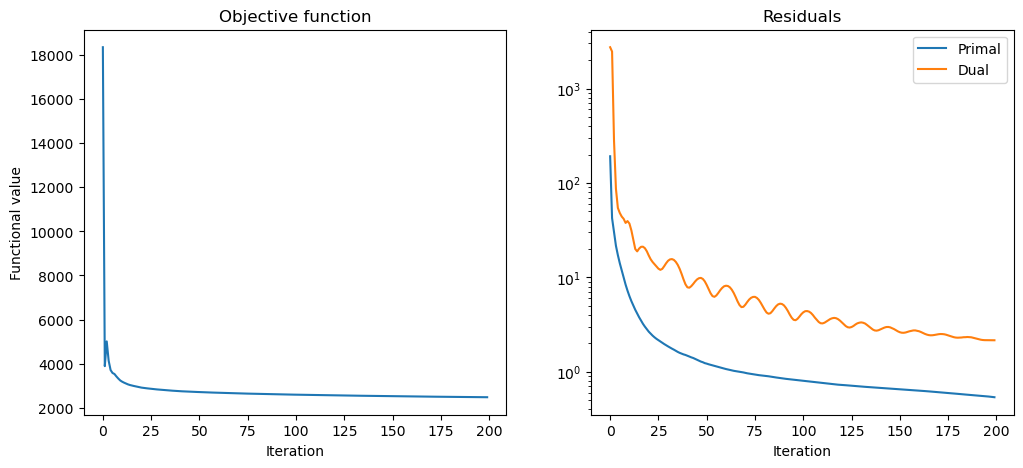
Plot convergence statistics.
[14]:
fig, ax = plot.subplots(nrows=1, ncols=2, figsize=(12, 5))
plot.plot(
hist.Objective,
title="Objective function",
xlbl="Iteration",
ylbl="Functional value",
fig=fig,
ax=ax[0],
)
plot.plot(
snp.vstack((hist.Prml_Rsdl, hist.Dual_Rsdl)).T,
ptyp="semilogy",
title="Residuals",
xlbl="Iteration",
lgnd=("Primal", "Dual"),
fig=fig,
ax=ax[1],
)
fig.show()