PPP (with DnCNN) Image Deconvolution (Proximal ADMM Solver)

This example demonstrates the solution of an image deconvolution problem using a proximal ADMM variant of the Plug-and-Play Priors (PPP) algorithm [50] with the DnCNN [58] denoiser.

import numpy as np

from xdesign import Foam, discrete_phantom

import scico.numpy as snp
from scico import functional, linop, loss, metric, plot, random
from scico.optimize import ProximalADMM
from scico.util import device_info
plot.config_notebook_plotting()

Create a ground truth image.

np.random.seed(1234)
N = 512  # image size
x_gt = discrete_phantom(Foam(size_range=[0.075, 0.0025], gap=1e-3, porosity=1), size=N)
x_gt = snp.array(x_gt)  # convert to jax array

Set up forward operator \(A\) and test signal consisting of blurred signal with additive Gaussian noise.

n = 5  # convolution kernel size
σ = 20.0 / 255  # noise level

psf = snp.ones((n, n)) / (n * n)
A = linop.Convolve(h=psf, input_shape=x_gt.shape)

Ax = A(x_gt)  # blurred image
noise, key = random.randn(Ax.shape)
y = Ax + σ * noise

Set up the problem to be solved. We want to minimize the functional

\[\mathrm{argmin}_{\mathbf{x}} \; (1/2) \| \mathbf{y} - A \mathbf{x} \|_2^2 + R(\mathbf{x}) \;\]

where \(R(\cdot)\) is a pseudo-functional having the DnCNN denoiser as its proximal operator. A slightly unusual variable splitting is used,

including setting the \(f\) functional to the \(R(\cdot)\) term and the \(g\) functional to the data fidelity term to allow the use of proximal ADMM, which avoids the need for conjugate gradient sub-iterations in the solver steps.

f = functional.DnCNN(variant="17M")
g = loss.SquaredL2Loss(y=y)

Set up proximal ADMM solver.

ρ = 0.2  # ADMM penalty parameter
maxiter = 10  # number of proximal ADMM iterations
mu, nu = ProximalADMM.estimate_parameters(A)

solver = ProximalADMM(
    f=f,
    g=g,
    A=A,
    rho=ρ,
    mu=mu,
    nu=nu,
    x0=A.T @ y,
    maxiter=maxiter,
    itstat_options={"display": True},
)

Run the solver.

print(f"Solving on {device_info()}\n")
x = solver.solve()
x = snp.clip(x, 0, 1)
hist = solver.itstat_object.history(transpose=True)

Solving on GPU (NVIDIA GeForce RTX 2080 Ti)

Iter  Time      Prml Rsdl  Dual Rsdl
------------------------------------
   0  1.87e+00  4.320e+01  2.631e+02
   1  2.09e+00  2.946e+01  5.875e+00
   2  2.29e+00  2.433e+01  4.868e+00
   3  2.49e+00  2.039e+01  4.079e+00
   4  2.69e+00  1.701e+01  3.403e+00
   5  2.90e+00  1.412e+01  2.825e+00
   6  3.10e+00  1.172e+01  2.345e+00
   7  3.30e+00  9.744e+00  1.950e+00
   8  3.50e+00  8.121e+00  1.625e+00
   9  3.70e+00  6.782e+00  1.357e+00

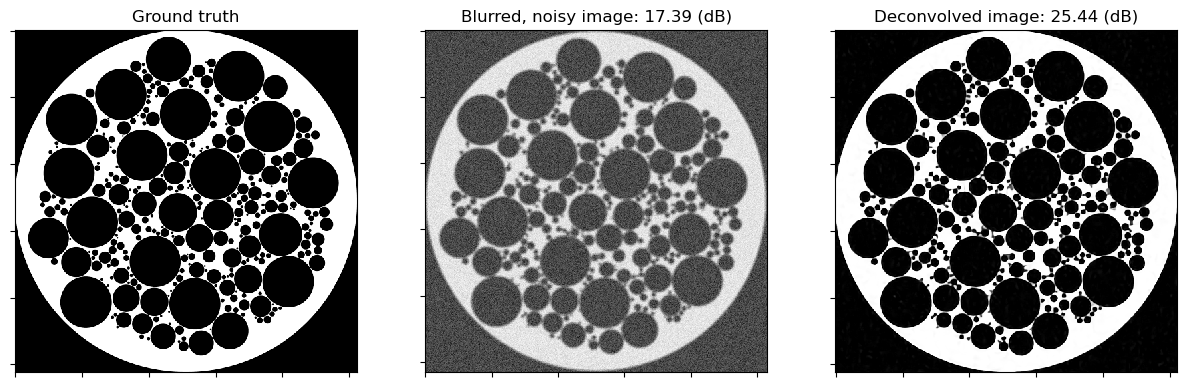
Show the recovered image.

fig, ax = plot.subplots(nrows=1, ncols=3, figsize=(15, 5))
plot.imview(x_gt, title="Ground truth", fig=fig, ax=ax[0])
nc = n // 2
yc = snp.clip(y[nc:-nc, nc:-nc], 0, 1)
plot.imview(y, title="Blurred, noisy image: %.2f (dB)" % metric.psnr(x_gt, yc), fig=fig, ax=ax[1])
plot.imview(x, title="Deconvolved image: %.2f (dB)" % metric.psnr(x_gt, x), fig=fig, ax=ax[2])
fig.show()

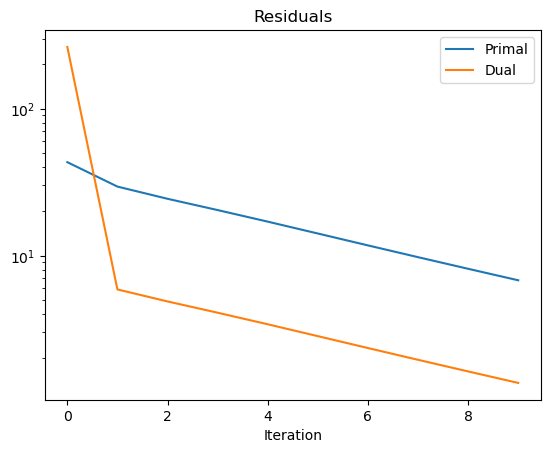
Plot convergence statistics.

plot.plot(
    snp.vstack((hist.Prml_Rsdl, hist.Dual_Rsdl)).T,
    ptyp="semilogy",
    title="Residuals",
    xlbl="Iteration",
    lgnd=("Primal", "Dual"),
)