Convolutional Sparse Coding (ADMM)#
This example demonstrates the solution of a simple convolutional sparse coding problem
where the \(\mathbf{h}\)_k is a set of filters comprising the dictionary, the \(\mathbf{x}\)_k is a corrresponding set of coefficient maps, and \(\mathbf{y}\) is the signal to be represented. The problem is solved via an ADMM algorithm using the frequency-domain approach proposed in [53].
[1]:
import numpy as np
import scico.numpy as snp
from scico import plot
from scico.examples import create_conv_sparse_phantom
from scico.functional import L1MinusL2Norm
from scico.linop import CircularConvolve, Identity, Sum
from scico.loss import SquaredL2Loss
from scico.optimize.admm import ADMM, FBlockCircularConvolveSolver
from scico.util import device_info
plot.config_notebook_plotting()
Set problem size and create random convolutional dictionary (a set of filters) and a corresponding sparse random set of coefficient maps.
[2]:
N = 128 # image size
Nnz = 128 # number of non-zeros in coefficient maps
h, x0 = create_conv_sparse_phantom(N, Nnz)
Normalize dictionary filters and scale coefficient maps accordingly.
[3]:
hnorm = np.sqrt(np.sum(h**2, axis=(1, 2), keepdims=True))
h /= hnorm
x0 *= hnorm
Convert numpy arrays to jax arrays.
[4]:
h = snp.array(h)
x0 = snp.array(x0)
Set up sum-of-convolutions forward operator.
[5]:
C = CircularConvolve(h, input_shape=x0.shape, ndims=2)
S = Sum(input_shape=C.output_shape, axis=0)
A = S @ C
Construct test image from dictionary \(\mathbf{h}\) and coefficient maps \(\mathbf{x}_0\).
[6]:
y = A(x0)
Set functional and solver parameters.
[7]:
λ = 1e0 # l1-l2 norm regularization parameter
ρ = 2e0 # ADMM penalty parameter
maxiter = 200 # number of ADMM iterations
Define loss function and regularization. Note the use of the \(\ell_1 - \ell_2\) norm, which has been found to provide slightly better performance than the \(\ell_1\) norm in this type of problem [54].
[8]:
f = SquaredL2Loss(y=y, A=A)
g0 = λ * L1MinusL2Norm()
C0 = Identity(input_shape=x0.shape)
Initialize ADMM solver.
[9]:
solver = ADMM(
f=f,
g_list=[g0],
C_list=[C0],
rho_list=[ρ],
alpha=1.8,
maxiter=maxiter,
subproblem_solver=FBlockCircularConvolveSolver(check_solve=True),
itstat_options={"display": True, "period": 10},
)
Run the solver.
[10]:
print(f"Solving on {device_info()}\n")
x1 = solver.solve()
hist = solver.itstat_object.history(transpose=True)
Solving on CPU
Iter Time Objective Prml Rsdl Dual Rsdl Slv Res
----------------------------------------------------------
0 3.16e-01 2.107e+03 3.851e+01 5.291e+01 7.229e-06
10 5.43e-01 2.862e+03 4.623e+00 9.837e+00 4.373e-06
20 6.30e-01 2.702e+03 2.097e+00 6.156e+00 5.701e-06
30 7.05e-01 2.626e+03 1.528e+00 4.603e+00 6.200e-06
40 7.77e-01 2.578e+03 1.222e+00 3.719e+00 8.564e-06
50 8.50e-01 2.542e+03 1.124e+00 3.478e+00 7.865e-06
60 9.25e-01 2.511e+03 1.053e+00 3.260e+00 1.318e-05
70 1.00e+00 2.486e+03 9.754e-01 3.012e+00 1.255e-05
80 1.08e+00 2.464e+03 8.965e-01 2.773e+00 5.969e-06
90 1.16e+00 2.444e+03 8.411e-01 2.613e+00 1.022e-05
100 1.24e+00 2.426e+03 8.010e-01 2.495e+00 1.429e-05
110 1.32e+00 2.411e+03 7.589e-01 2.367e+00 8.354e-06
120 1.40e+00 2.398e+03 7.139e-01 2.224e+00 1.338e-05
130 1.48e+00 2.386e+03 6.680e-01 2.077e+00 1.682e-05
140 1.57e+00 2.377e+03 6.111e-01 1.881e+00 1.240e-05
150 1.65e+00 2.368e+03 5.547e-01 1.717e+00 4.472e-06
160 1.74e+00 2.361e+03 5.135e-01 1.595e+00 7.214e-06
170 1.82e+00 2.356e+03 4.665e-01 1.439e+00 9.240e-06
180 1.90e+00 2.352e+03 4.243e-01 1.301e+00 5.187e-06
190 1.97e+00 2.348e+03 3.730e-01 1.135e+00 9.683e-06
199 2.05e+00 2.347e+03 3.064e-01 8.974e-01 6.658e-06
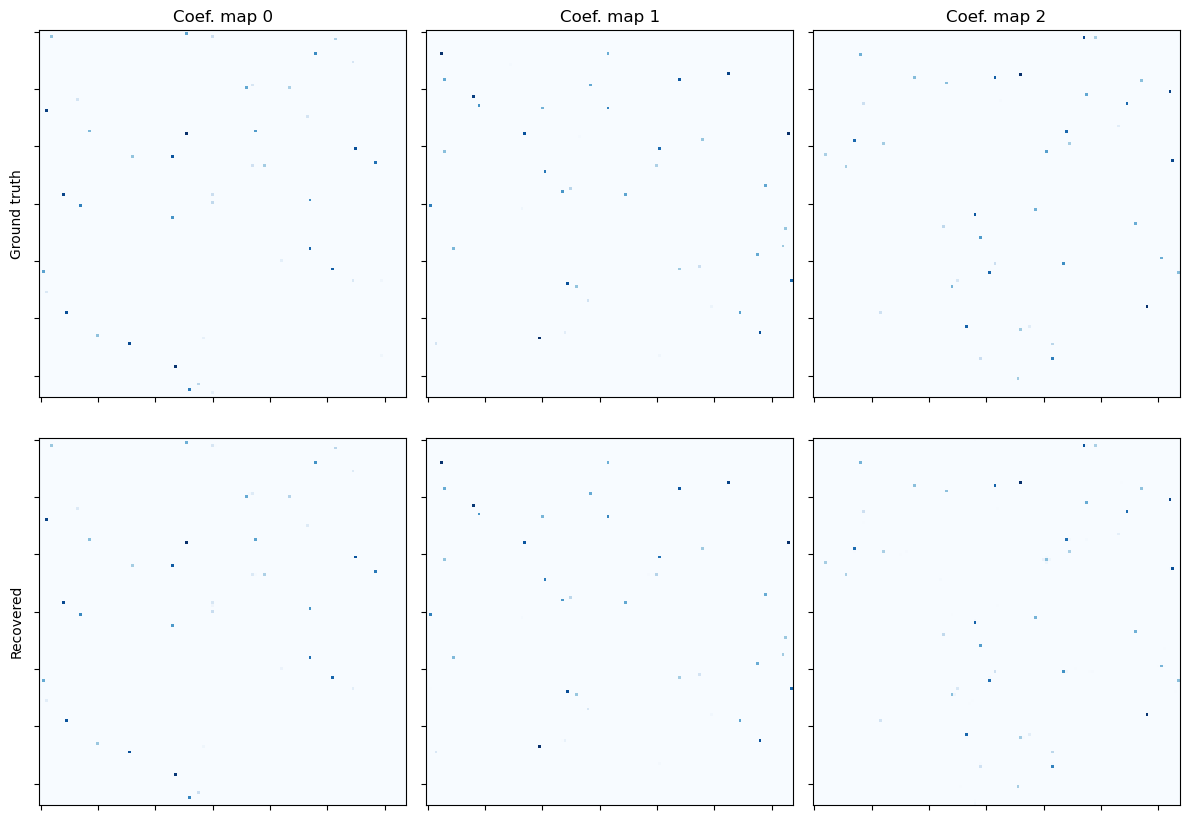
Show the recovered coefficient maps.
[11]:
fig, ax = plot.subplots(nrows=2, ncols=3, figsize=(12, 8.6))
plot.imview(x0[0], title="Coef. map 0", cmap=plot.cm.Blues, fig=fig, ax=ax[0, 0])
ax[0, 0].set_ylabel("Ground truth")
plot.imview(x0[1], title="Coef. map 1", cmap=plot.cm.Blues, fig=fig, ax=ax[0, 1])
plot.imview(x0[2], title="Coef. map 2", cmap=plot.cm.Blues, fig=fig, ax=ax[0, 2])
plot.imview(x1[0], cmap=plot.cm.Blues, fig=fig, ax=ax[1, 0])
ax[1, 0].set_ylabel("Recovered")
plot.imview(x1[1], cmap=plot.cm.Blues, fig=fig, ax=ax[1, 1])
plot.imview(x1[2], cmap=plot.cm.Blues, fig=fig, ax=ax[1, 2])
fig.tight_layout()
fig.show()
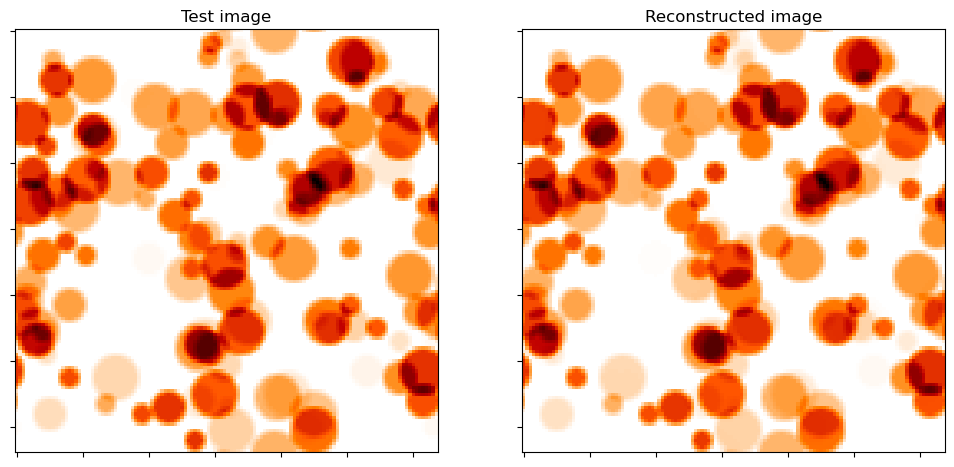
Show test image and reconstruction from recovered coefficient maps.
[12]:
fig, ax = plot.subplots(nrows=1, ncols=2, figsize=(12, 6))
plot.imview(y, title="Test image", cmap=plot.cm.gist_heat_r, fig=fig, ax=ax[0])
plot.imview(A(x1), title="Reconstructed image", cmap=plot.cm.gist_heat_r, fig=fig, ax=ax[1])
fig.show()
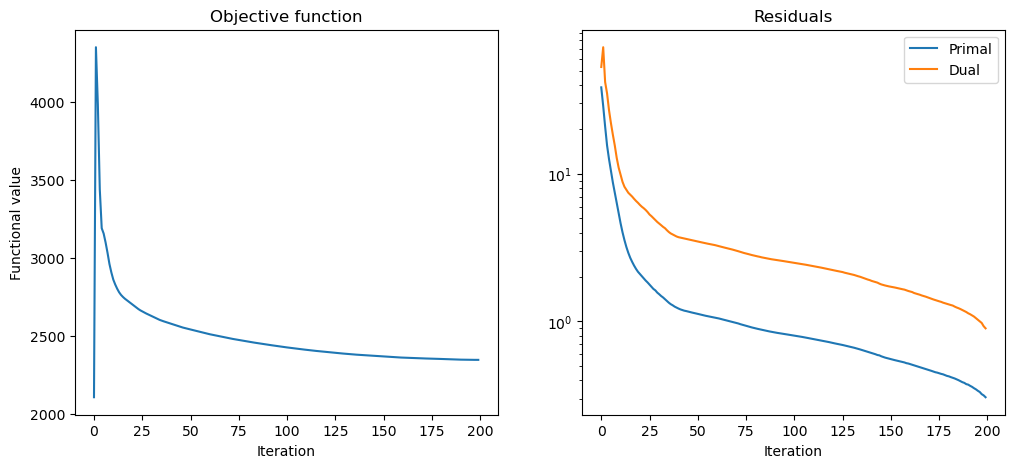
Plot convergence statistics.
[13]:
fig, ax = plot.subplots(nrows=1, ncols=2, figsize=(12, 5))
plot.plot(
hist.Objective,
title="Objective function",
xlbl="Iteration",
ylbl="Functional value",
fig=fig,
ax=ax[0],
)
plot.plot(
snp.vstack((hist.Prml_Rsdl, hist.Dual_Rsdl)).T,
ptyp="semilogy",
title="Residuals",
xlbl="Iteration",
lgnd=("Primal", "Dual"),
fig=fig,
ax=ax[1],
)
fig.show()