Image Deconvolution with TV Regularization (ADMM Solver)#
This example demonstrates the solution of an image deconvolution problem with isotropic total variation (TV) regularization
where \(C\) is a convolution operator, \(\mathbf{y}\) is the blurred image, \(D\) is a 2D finite fifference operator, and \(\mathbf{x}\) is the deconvolved image.
In this example the problem is solved via standard ADMM, while proximal ADMM is used in a companion example.
[1]:
from xdesign import SiemensStar, discrete_phantom
import scico.numpy as snp
import scico.random
from scico import functional, linop, loss, metric, plot
from scico.optimize.admm import ADMM, LinearSubproblemSolver
from scico.util import device_info
plot.config_notebook_plotting()
Create a ground truth image.
[2]:
phantom = SiemensStar(32)
N = 256 # image size
x_gt = snp.pad(discrete_phantom(phantom, N - 16), 8)
Set up the forward operator and create a test signal consisting of a blurred signal with additive Gaussian noise.
[3]:
n = 5 # convolution kernel size
σ = 20.0 / 255 # noise level
psf = snp.ones((n, n)) / (n * n)
C = linop.Convolve(h=psf, input_shape=x_gt.shape)
Cx = C(x_gt) # blurred image
noise, key = scico.random.randn(Cx.shape, seed=0)
y = Cx + σ * noise
Set up the problem to be solved. We want to minimize the functional
where \(C\) is the convolution operator and \(D\) is a finite difference operator. This problem can be expressed as
which is easily written in the form of a standard ADMM problem.
This is simpler splitting than that used in the companion example, but it requires the use conjugate gradient sub-iterations to solve the ADMM step associated with the data fidelity term.
[4]:
f = loss.SquaredL2Loss(y=y, A=C)
# Penalty parameters must be accounted for in the gi functions, not as
# additional inputs.
λ = 2.1e-2 # L21 norm regularization parameter
g = λ * functional.L21Norm()
# The append=0 option makes the results of horizontal and vertical
# finite differences the same shape, which is required for the L21Norm,
# which is used so that g(Cx) corresponds to isotropic TV.
D = linop.FiniteDifference(input_shape=x_gt.shape, append=0)
Set up an ADMM solver object.
[5]:
ρ = 1.0e-1 # ADMM penalty parameter
maxiter = 50 # number of ADMM iterations
solver = ADMM(
f=f,
g_list=[g],
C_list=[D],
rho_list=[ρ],
x0=C.adj(y),
maxiter=maxiter,
subproblem_solver=LinearSubproblemSolver(),
itstat_options={"display": True, "period": 10},
)
Run the solver.
[6]:
print(f"Solving on {device_info()}\n")
x = solver.solve()
hist = solver.itstat_object.history(transpose=True)
Solving on GPU (NVIDIA GeForce RTX 2080 Ti)
Iter Time Objective Prml Rsdl Dual Rsdl CG It CG Res
-----------------------------------------------------------------
0 3.17e+00 2.230e+02 3.401e+01 1.253e+01 9 6.977e-05
10 4.68e+00 3.316e+02 1.256e+00 2.705e+00 4 9.068e-05
20 4.81e+00 3.324e+02 5.717e-01 1.118e+00 3 7.155e-05
30 4.90e+00 3.327e+02 3.462e-01 6.393e-01 2 7.551e-05
40 5.00e+00 3.329e+02 2.415e-01 3.947e-01 1 9.663e-05
49 5.07e+00 3.330e+02 1.857e-01 2.918e-01 1 8.986e-05
Show the recovered image.
[7]:
fig, ax = plot.subplots(nrows=1, ncols=3, figsize=(15, 5))
plot.imview(x_gt, title="Ground truth", fig=fig, ax=ax[0])
nc = n // 2
yc = y[nc:-nc, nc:-nc]
plot.imview(y, title="Blurred, noisy image: %.2f (dB)" % metric.psnr(x_gt, yc), fig=fig, ax=ax[1])
plot.imview(
solver.x, title="Deconvolved image: %.2f (dB)" % metric.psnr(x_gt, solver.x), fig=fig, ax=ax[2]
)
fig.show()

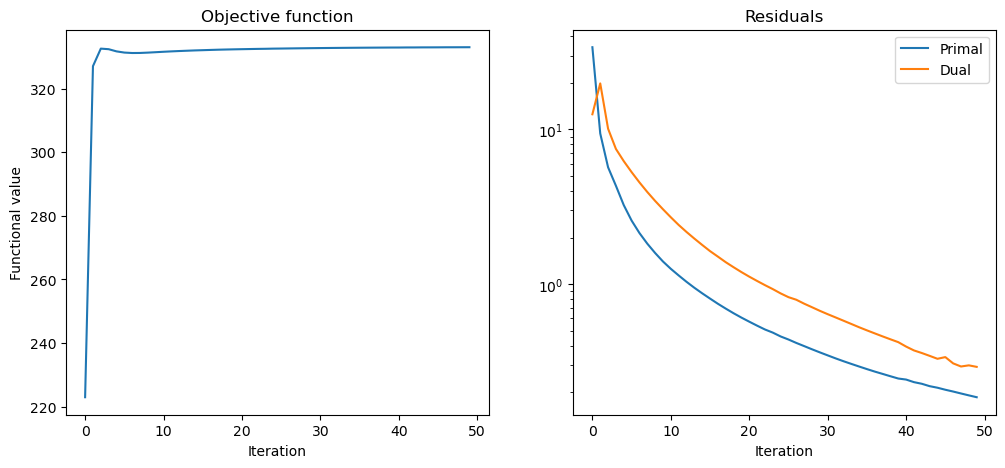
Plot convergence statistics.
[8]:
fig, ax = plot.subplots(nrows=1, ncols=2, figsize=(12, 5))
plot.plot(
hist.Objective,
title="Objective function",
xlbl="Iteration",
ylbl="Functional value",
fig=fig,
ax=ax[0],
)
plot.plot(
snp.vstack((hist.Prml_Rsdl, hist.Dual_Rsdl)).T,
ptyp="semilogy",
title="Residuals",
xlbl="Iteration",
lgnd=("Primal", "Dual"),
fig=fig,
ax=ax[1],
)
fig.show()